 |
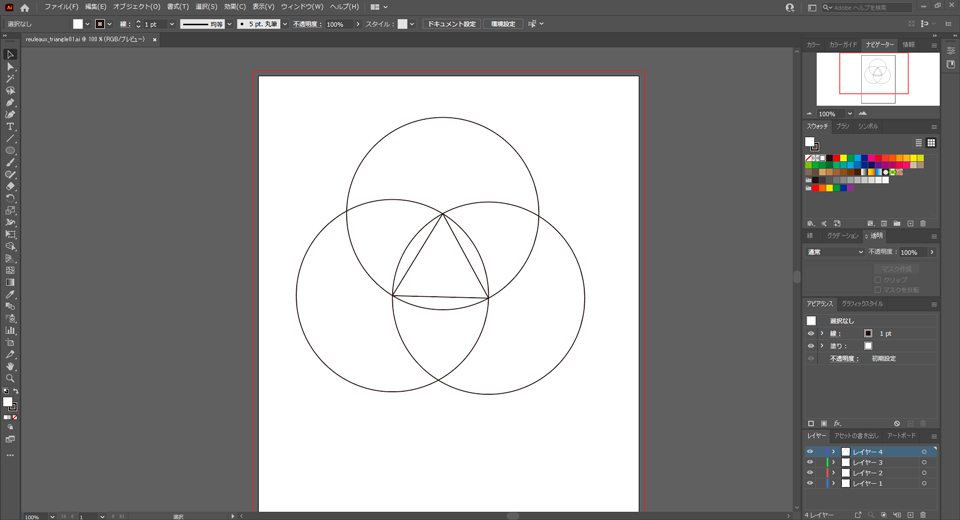
| 【イラレで描いたルーローの三角形(中央部)】 |
先日、ある医院で新型コロナ(COVID-19)のワクチン接種をした際、看護師さんが私の左腕に貼り付けた絆創膏は、およそ1cm角の正方形に中央の丸い円の形をした不織布製パッドの付いたものであった。ごく普通の絆創膏である。その夜、私は思い出したかのように左腕に貼られていた絆創膏を眺め、程なくしてそれを剥がしたのだった――。
まるで小さな電子部品のボタンスイッチのような形をした絆創膏は、注射針が刺さった際の患部を平穏無事に保護してくれていたわけであり、なんとなくその誇らしげな絆創膏が視界から消えてしまったのを、私は心許なく寂しく思った。
絆創膏に見た、丸い円…。まことに唐突ながら、ここから円の話をしていきたい――。
円とは、言うまでもなく丸いこと、丸い形のものを指す。ちなみに三省堂の『新明解国語辞典』では、次のような理知的な表現で語意と解釈が記されていた。《コンパスを使って描いた図形のように、どの部分も同一の曲がり具合だと認められる曲線》。円について、少しばかりこのような数学的な世界に浸ってみたい。
➤個人的な円にまつわる記憶
小学5年の算数で円周率を習い、6年で円の面積を習う。だがそれ以前に、私の中で、円に関する記憶というのがある。
最も遠い彼方にある円の記憶は、幼少の頃、小学生だった姉が所有していた、透明なプラスチック製のスピログラフ(Spirograph)である。スピログラフとは、曲線の幾何学模様を描くための定規で、紙切れだったかノートだったかは憶えていないが、このスピログラフの定規を使って姉が描き残したのだろう幾何学模様を眺めたのを、かすかに憶えている。それはたいへん美しいアートでもあった。
さらに円にまつわる印象深い記憶というのは、こんなところにもある。
かつてフジテレビ系列の歌番組で、『夜のヒットスタジオ』(司会は井上順、芳村真理)というのがあった。毎週多才なシンガーやグループが登場し、歌を歌い、和気藹々とした明るい雰囲気でポップスやロックや演歌の音楽世界が繰り広げられた。その番組のスタジオ・セット(背景、書き割り)となっていた、アクリル装飾の造形デザインが、黒と白の円のパターン・グラフィックなのであった。
このパターン・グラフィックのデザインは、日本人の美術スタッフの造形なのだけれど、どことなく、ハンガリー系フランス人の芸術家ヴィクトル・ヴァザルリ(Victor Vasarely)の「ノワール・ムーヴ」によく似ていたわけである。
ヴィクトル・ヴァザルリの描いた円形パターンの抽象性はどうやら、ドイツ(ヴァイマル共和政時代)のバウハウスの構成主義に通ずるものらしく、こういった円形を用いた抽象的な装飾の趣は、現行の一般的なテレビ番組の美術ではほとんど見られなくなってしまった。
以前のテレビメディアは、こうした芸術的な側面がスタッフのセンスと技術力によって引き出されていた感があるが、現行においては、ほとんどアニメーションとモーション・ピクチャーによって演出が施され、そのためスタジオ・セットはグリーン・バックであったり、そうでなければ非抽象的な、現実感のある建造物を模し、かなり大袈裟な装飾(花やオブジェ)を施しているいる場合が多く、したがって昭和であった私の少年時代、『夜のヒットスタジオ』のような、一貫した抽象的デザインのモチーフを視覚的にとらえてきたことによって、鮮烈なる――とくに円形にまつわる――芸術的指向性にくすぐられる感覚が、ずいぶんと養われた気がするのである。
 |
| 【ポザマンティエとゲレトシュレーガーの著書『円をめぐる冒険 幾何学から文化史まで』】 |
➤ポザマンティエとゲレトシュレーガーの『円をめぐる冒険』
何故こうしたまでに円の図形の話をことさら興奮気味に述べているのかと言えば、ニューヨーク市立大学シティカレッジ名誉教授で数学研究者のアルフレッド・S.ポザマンティエ(Alfred S.Posamentier)とオーストリアの高校数学教師のロベルト・ゲレトシュレーガー(Robert Geretschläger)の著書である『円をめぐる冒険 幾何学から文化史まで』(松浦俊輔訳、紀伊國屋書店)を読んだからである。
近頃私は、Adobeのイラレ(Illustrator)を使って創作上、円を描くことが多い。そこで、試しにこういう本を嗜んでみたらどうだろうと思ったのがきっかけだったのだが、なかなかどうして難解な本である。
この本の装幀にある円の図形は、いったい何を表したものか。これは、円の対称となる「反転」について述べられた章の中の解説図形なのである。言葉にするとなかなか難しいのだが、対称すなわち「鏡映」の概念の話であり、基準となる円がある法則によって反転(鏡映化)した円と重なる時、それは(反転の)拡張という概念に駆られて、複数の円の作図上のアポロニウスの問題をはらみつつも(理論上)解決されていく――という解説のための図形――である。この説明が正しいかどうか、全く自信がない。
実際にイラレを使って、例えば複数の円で何かしらのイラストを構築しようとする時、意外なほど「反転」の概念に触れる作図法によって、複雑なイラストの構築が可能となる場合があり、こうした数理のいろいろが、美術の制作上、決して蚊帳の外にあるわけではなく、積極的に用いられていることを端的に物語っているのである。
『円をめぐる冒険 幾何学から文化史まで』という本は、道理に外れることなく満遍なく、数学上の数理というか定理というか、そういった数式が無数に鏤められていて、読書の観点で言うと、ちょっと難しくて困ってしまう本である。しかしながら、数学というか円の世界は面白いのだ。
円というのは、子供でも認識できるくらいに単純な姿をしていながら、その内実、この世のすべて――すなわち宇宙を含めた万物――を統治しているのではないか、とすら思えてくるような、全く理知に富んだ哲学的実相に溢れているのである。辿っていくと難解ではあるにせよ、円には親しみやすい特性がある。だから私は少々、円について興味をかじり、興奮気味になってしまうのであった。
 |
| 【第1章「基礎と拡張」に登場するルーローの三角形】 |
➤ルーローの三角形
私にとって円における数学的あるいは造形美の最大の関心事は――学生時代の話だけれど――ルーローの三角形(Reuleaux triangle)であった。これは間違いない。
これほど美しい三角形はないだろうと、かつて率直に感動したわけである。ルーローの三角形とは何かについて、『円をめぐる冒険 幾何学から文化史まで』の中の文章を引用して説明すると、《ルーローの三角形は、半径が等しく、正三角形の各頂点を中心とする3本の円弧でできている。多くの変わった性質があり、幅が同じ円によく似ている》ということになる。ちなみにこの魅惑の性質のある三角形は、木製の玩具にもなって販売されており、子供達の興味を惹く特別な印象のある図形――ということも言える。
三角形?――円の話をしているのに三角形とはいったいどういうことなのか?――ということを説明しなければならない。だが、ルーローの三角形について知っている人ならば、これはもう自明である。
ドイツの機械工学者のフランツ・ルーロー(Franz Reuleaux)という人が、これを考察した――という。尤も、私が感動したのは、厳密に言うと図形としてのルーローの三角形ではなく、その頃――工業高校時代に遡って――の機械科の教室だったか作業室だったかで見た、ロータリーエンジンの模型の造形の美しさであった。
工業高校生ならばこれも自明であり、ロータリーエンジンと聞けばピンとくるものなのである。円というのは、転がした時に高さが変わらない、いわゆる「定幅図形」である。この3辺が丸みを帯びたルーローの三角形も、同じく「定幅図形」なのである。転がした時に高さが変わらないというのが、工業製品としてみると、たいへん旨みのあるものなのだ。
その昔、ピストン式エンジンとは別の型による、燃料消費にともなう効率化の開発競争において、このルーローの三角形を取り入れたエンジンの機構が具現化された。日本で特に有名なのがマツダのロータリーエンジンだろう。ローターの仕組みとしては、以下、Wikipediaの解説を引用しておく。
《ピストンとコネクティングロッドに相当するもので、ローターハウジングのトロコイド曲線に内接する3葉の内包絡線で構成された、三角形(ルーローの三角形)をしたもの。中心にはローターベアリングを介してエキセントリックシャフトがはめられる丸い穴部があり、その縁にはサイドハウジングのギヤ部とかみ合う内歯の歯型(インターナルギヤ)が設けられている。自動車ファンの間では「おにぎり」と称される事もある》
(Wikipedia「ロータリーエンジン」より引用)
もはや実直かつ明解なこととして、図形的美しさを秘めたルーローの三角形に、ある種のフェティシズム的な魅力を感じたりはしないだろうか。『円をめぐる冒険 幾何学から文化史まで』の本に記されていたルーローの三角形の図形を真似して、実際にAdobeのイラレでルーローの三角形を描いてみたのである。
これほど美しい図形はないだろう。三角形の3つの頂点を所有していながら、それを結ぶ3辺が惑溺するほど柔らかい曲線で描かれるのだから、理知を飛び越えた聖なる美しさとも表現したくなる。――男性の人体の一部分に、これとよく似た形状を見た…と気づく人は多くいるのではないか。そう、その通りである。ここではその手の話の言及を省くことにするが、しかしながらルーローの三角形は、今やその存在をどこにでも発見できそうな気がする。
さて、前述した「ノワール・ムーヴ」に近いパターン・デザインで、そのモチーフを円ではなく、ルーローの三角形にしたらどうだろう――というのを、私はイラレで描いてみようと思った。
これの結果についても、たいへん話が長くなりそうなので、割愛させていただく。いずれ、私の創作作品に、そのようなパターン・デザインが紛れ込んで登場するかも知れないが、関心のある方はどうぞ注意深く、ご鑑賞いただければと思う。円の話を終わりにする。


コメント